How EDI differs from Fourier Transform Spectroscopy (FTS)

EDI differs from FTS by....

1. Using CCDs to accumulate counts
   --does not require time dependent recording channels

2. 10x - 100x better photon signal/noise ratio
   -- can do FAINT SOURCE astronomy

3. Non-scanning delay
   --can record TRANSIENT phenomena

Discussion of #2, why EDI has better photon signal to noise ratio

Both EDI and FTS measure an interferogram, and then convert the interferogram via the Fourier transform to wavelength (actually, wavenumber) space. The difference is in what manner is the interferogram is measured.

The EDI measures the interferogram in a few widely spaced segments, whereas the FTS measures the interferogram in very numerous infinitely narrow segments. The red region below represents the width of the segment that the instrument can measure instantaneously. This is proportional to the spectral resolution of the disperser. Since the FTS has no disperser its instantaneous spectral resolution is zero so the red segment becomes an infinitely narrow spike. Thus whereas the EDI can measure the entire interferogram in a few segments (which can be done simultaneously in some configurations, see below) the FTS must scan through many exposures, which takes time.

The amount of information that is obtained in a single exposure grows with the number of wavelength channels. The FTS has no dispersion and so there is a single wavelength channel. The EDI can have several thousand wavelength channels per exposure.

You can simulate the FTS result from the EDI data by summing together all the wavelength channels into a single channel. Because the phases of the various fringes are randomly distributed, the fringe visibility of the sum will be reduced by a factor of about the square root of the number of wavelength channels in the EDI detector. Hence, the photon limited signal to noise of the EDI is better than the FTS by a factor of the square root of the number of wavelength channels. Since the number of CCD pixels can be several thousand, this is a factor of 10x to 100x improvement.

This allows the EDI to be used with faint source astronomy. Currently the FTS is not practical for optical astronomy because its photon signal to noise ratio is so poor. (Instead it is used primarily in the infrared where the number of photons per milliwatt of light is much greater.) Thus by adding dispersion, the FTS can be used (as an EDI) for optical astronomy, and it brings the advantage, common to interferometers, of robust instrument response insensitive to pupil shape.

Discussion of #3, how EDI can measure transient phenomena such as in explosions etc.

Since the FTS requires time to scan the interferometer over the desired delay, it cannot be used to measure transient events that are brief relative to the scan time.

In contrast, the EDI can measure brief phenomena because it only has one-to-a-few interferometer delays to use, and it can measure these simultaneously when the apparatus is arranged as shown in the diagram below.

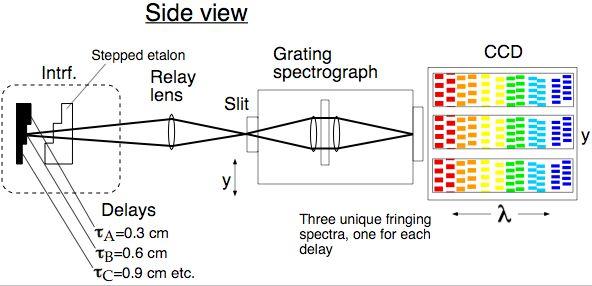
The thicknesses of the etalon and mirror are stepped to provide different delay amounts, and chosen so that the virtual image of the mirror appears in the same plane for all steps. This preserves the wide angle ability of the interferometer (useful for extended sources and uncollimated beams). Each step of the mirror creates a different interferometer delay, and all the delays can be recorded simultaneously on the same spectrograph and CCD chip.

The beamsplitter portion of the interferometer has been omitted in the above cartoon.

www.SpectralFringe.org site maintained by
David Erskine
erskine1@llnl.gov

Back to EDI home